测试过程中,我们经常遇到需要覆盖多个变化参数的测试场景,如我们测试一个设备通道视频参数设置的各种组合测试,如下图:

多数情况下,类似于这种多组合测试时,老员工则是依靠经验去进行有针对性的测试,而我们新员工会随机的乱点一通看能否正常保存成功,看看相应的视频文件是否符合设置,幸运的话,能发现几个bug。这种方式不但不科学,而且测试覆盖面也很窄,这里可以使用常见的两种方法进行测试用例的分析和设计:组合分析方法和正交实验设计方法。(均以上图为例)
1.用组合分析方法进行测试用例设计:
关于组合分析方法,依据的是多因素组合测试可以生成测试用例集,以覆盖任意N个因素的所有取值组合,在理论上可以发现由N个因素共同作用引发的缺陷。简单的理解就是每一个参数的每一个值只需要和其他参数至少配对一次就够了。
上面的因子及各因子状态如下:
码流类别:主码流,子码流,事件参数
码流类型:复合流,视频流
分辨率:DCIF,CIF,QCIF,2CIF,4CIF,保留,VGA,UXGA,HD720P
#这个设置要根据前段设备的型号,有的设备不支持较大的分辨率
图像质量:最好,较好,次好,一般,较差,差
码率类型:定码率,变码率
视频码率:32Kbps,320Kbps,2048Kbps #对于这个设置可以随机选择几个进行测试
视频帧率:全帧率,1/16,1/4,1,10,20 #对于这个设置可以随机选择几个进行测试
帧类型:单P帧,BBP帧,BP帧
I帧间隔:0,200,400 #由于I帧间隔的范围0—400,我们随机选择三个
按照传统思路,这些参数的排列组合有:3*2*9*6*2*3*6*3*3=104976,也就是说我们要进行104976次测试的执行,这个在现实测试中是不可能实现的。我们用组合分析方法可以裁剪测试用例的数量,达到我们可接受的范围。
这里可以使用一个工具:PICT。具体操作步骤如下:
1. 先安装好PICT工
2. 建一个模型文件,文件是.txt格式,如:modelfiles.txt。针对上图文件内容如下:
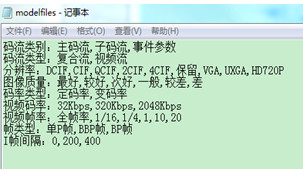
注意:文本文件中的“,”“:”都是英文字符
3. DOS窗口进入到PICT安装目录下,运行:Pict modelfiles.txt
注:若将测试因子的优化组合保存到安装目录下,且以*.txt格式显示,可输入命令C:\Program Files\PICT>pict modelfiles.txt > output.txt;也可以*.xls格式显示,可输入命令C:\Program Files\PICT>pict modelfiles.txt > output.xls
测试因子的优化组合如下:(由于.xls格式中输入1/16显示1月16日,也即1/16不能在.xls中显示,这里以1\16代替1/16,其他类似)
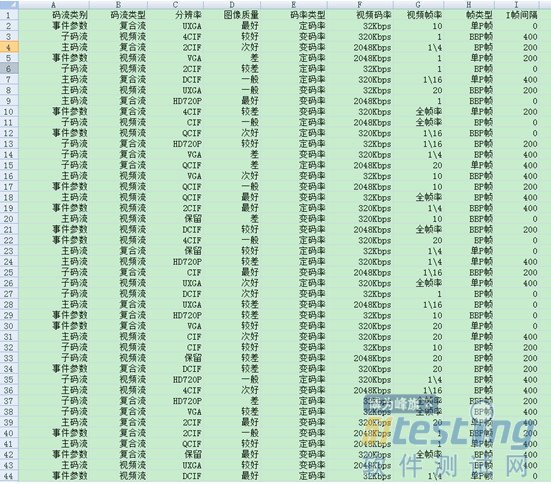
通过导出的.xls,我们知道,只需要执行60次测试用例即可达到104976次同样的效果。在测试中,我们可以在模型文件中加入一些条件语句限制一些特殊的情况,比如当视屏码率选择自定义时,自定义码率输入框不能为空等。对于有经验的人员可以在上面组合的基础上适当的加入一些容易出现问题的测试用例,增加测试的覆盖面。最近读《微软的软件测试之道》,里面也有关于组合测试的介绍,书中建议组合分析从两因素组合测试开始,逐渐提高组合维度,直至6因素组合测试,因为有研究表明6因素组合测试可以发现绝大多数的程序缺陷。
2.用正交分析方法设计(又称为两两组合)测试用例
所谓正交试验法,就是从大量的试验点中挑选出适量的,有代表性的点,合理的安排试验。
如果我们直接在上例中运用正交试验法,可能仍然达不到我们可以接受的范围,即测试用例还是很多。这时我们可以计算各因子和状态的权值,删去一部分权值较小,即重要性较小的因子或者状态,使最后生成的测试用例集缩减到我们可以接受的范围。
针对上例中,我们做如下修改(这里只是指出怎么应用正交试验法,所选修改以简便为主,实际中可根据需要删减):
码流类别:主码流=0,子码流=1
码流类型:复合流=0,视频流=1
分辨率:DCIF=0,CIF=1,QCIF=2,4CIF=3,保留=4
图像质量:最好=0,较好=1,次好=2,一般=3,差=4
视频帧率:全帧率=0,1/16=1,1/4=2,1=3,10=4,20=5
帧类型:单P帧=0,BBP帧=1,BP帧=2
根据上面分析情况,我们在常用正交矩阵表中,选择在保证因素数、水平数最接近但略大于实际值的基础上,选择行数最小的矩阵表。我们选择5^6的矩阵表:如下
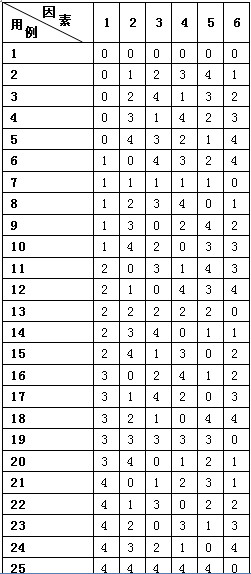
观察上面的结果就应该了解为什么叫两两组合了;使用正交表转换成测试用例时(即套用正交表时),只要将多出来的列删除即可,矩阵仍然符合正交矩阵的特性;对于多出来的行不能删除其中的任意一行,如上例中对于有些因子实际上所含的状态数小于5个,可以用确定的状态数去间隔性的填充范围外的状态(填充技巧:用客户端比较关注的参数值填充);
最后把因子实际的状态按照上面的规则填到正交试验表中,即可得到可接受的测试用例。
以上是用手工的方法进行正交设计的,当然我们也可以使用工具完成,常用的工具有:Allpairs(有点像PICT工具使用,dos命令下运行)和ACTS,其使用也很简便,这里不做介绍了。
Allpairs下载:www.satisfice.com/tools.shtml
Allpairs下载:http://csrc.nist.gov/groups/SNS/acts/documents/comparison-report.html#acts
这里对这两种方法做个比较小结:
1. 正交分析方法强调两两组合覆盖会覆盖到所有单参数、所有参数两两组合以及部分参数多组合的场景,会抛弃一些多组合场景。正交设计方法有利于确定各个因素对实验结果的贡献,但是对于组合测试提高错误检测能力并没有帮助。组合分析是随机生成的,它的原则是覆盖即可,多考虑覆盖多组合情况。
2. 组合分析法是一种基于每对参数组合的测试技术,考虑参数之间的影响是主要的错误来源,并且大多数的错误起源于简单的参数组合。但是对于单参数以及两两组合覆盖率不如正交设计方法。
3. 正交设计方法由于是基于两两组合,故对同一对象多次设计用例变化不是太大,而组合分析运用PICT可以很方便的获取一组测试数据,而且每组测试数据均不同,在回归测试中,可以很方便的运用另一组组合分析数据,提高测试覆盖率。
4. 运用正交试验分析和组合测试都需要对要测试的因子及因子状态有清楚的了解,并对其加权,哪些权值较重,哪些较轻,可以删减因子,减少测试用例数。具体运用哪种方法,要看具体测试对象,也要看测试人员自己的喜好。
5. 正交设计是组合设计的一个具体特例,也是组合测试的一种方案选择。
----------------------------------------------------------------------------------
转自:http://www.51testing.com/?uid-363907-action-viewspace-itemid-834664
作者:没吃饱的飞鱼
